Finite Volume Element Discretization for the incompressible Navier-Stokes Equation. More...

#include <navier_stokes_fv1.h>

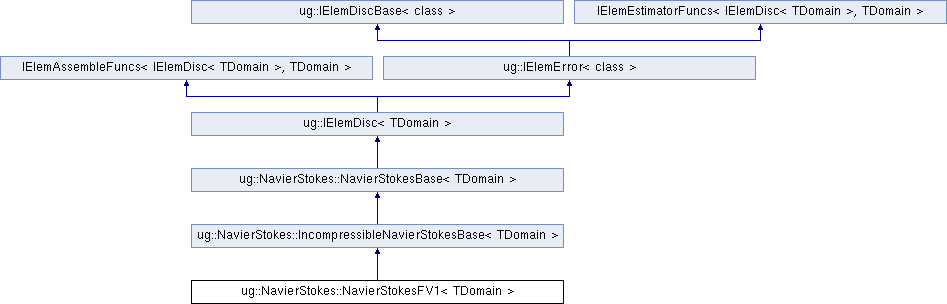
Inheritance diagram for ug::NavierStokes::NavierStokesFV1< TDomain >:

Public Member Functions
template<typename TElem , typename TFVGeom >
void	add_def_A_elem (LocalVector &d, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])
	adds the stiffness part to the local defect

template<typename TElem , typename TFVGeom >
void	add_def_M_elem (LocalVector &d, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])
	adds the mass part to the local defect

template<typename TElem , typename TFVGeom >
void	add_jac_A_elem (LocalMatrix &J, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])
	adds the stiffness part to the local jacobian

template<typename TElem , typename TFVGeom >
void	add_jac_M_elem (LocalMatrix &J, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])
	adds the mass part to the local jacobian

template<typename TElem , typename TFVGeom >
void	add_rhs_elem (LocalVector &d, GridObject *elem, const MathVector< dim > vCornerCoords[])
	adds the source part to the local defect

SmartPtr< CplUserData< number, dim > >	density ()
	returns density

virtual std::string	disc_type () const
	returns string identifying disc type

template<typename TElem , typename TFVGeom >
void	ex_nodal_velocity (MathVector< dim > vValue[], const MathVector< dim > vGlobIP[], number time, int si, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const MathVector< TFVGeom::dim > vLocIP[], const size_t nip, bool bDeriv, std::vector< std::vector< MathVector< dim > > > vvvDeriv[])
	export value of the velocity

template<typename TElem , typename TFVGeom >
void	ex_velocity_grad (MathMatrix< dim, dim > vValue[], const MathVector< dim > vGlobIP[], number time, int si, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const MathVector< TFVGeom::dim > vLocIP[], const size_t nip, bool bDeriv, std::vector< std::vector< MathMatrix< dim, dim > > > vvvDeriv[])
	computes the value of the gradient of the velocity

template<typename TElem , typename TFVGeom >
void	fsh_elem_loop ()
	finishes the element loop

SmartPtr< CplUserData< number, dim > >	kinematic_viscosity ()
	returns kinematic viscosity

template<typename TFVGeom >
number	peclet_blend (MathVector< dim > &UpwindVel, const TFVGeom &geo, size_t ip, const MathVector< dim > &StdVel, number kinVisco)
	computes the pecled blended Upwind veloctity

template<typename TElem , typename TFVGeom >
void	prep_elem (const LocalVector &u, GridObject *elem, const ReferenceObjectID roid, const MathVector< dim > vCornerCoords[])
	prepares the element for evaluation

template<typename TElem , typename TFVGeom >
void	prep_elem_loop (const ReferenceObjectID roid, const int si)
	prepares the element loop

virtual void	prepare_setting (const std::vector< LFEID > &vLfeID, bool bNonRegularGrid)
	type of trial space for each function used

void	set_density (SmartPtr< CplUserData< number, dim > > user)
	sets the density

void	set_kinematic_viscosity (SmartPtr< CplUserData< number, dim > > user)
	sets the kinematic viscosity

void	set_pac_upwind (bool bPac)

void	set_source (SmartPtr< CplUserData< MathVector< dim >, dim > > user)
	sets the source function

void	set_stabilization (const std::string &name)
	sets stabilization based on string identifier

void	set_stabilization (const std::string &name, const std::string &diffLength)
	sets stabilization and diff length method based on string identifier (only for Schneider-Raw stabilizations)

void	set_stabilization (SmartPtr< INavierStokesFV1Stabilization< dim > > spStab)
	sets the stabilization used to compute the stabilized velocities

void	set_upwind (const std::string &name)
	sets the upwind based on a string identifier

void	set_upwind (SmartPtr< INavierStokesFV1Stabilization< dim > > spStab)
	sets a stabilization for upwinding (Physical Advection Correction)

void	set_upwind (SmartPtr< INavierStokesUpwind< dim > > spUpwind)
	sets an upwinding for the convective term of momentum equation

DataImport< MathVector< dim >, dim >	sourceSCVF ()
	returns scvf source

SmartPtr< INavierStokesFV1Stabilization< dim > >	stabilization ()
	returns stabilization


	NavierStokesFV1 (const char functions, const char subsets)

	NavierStokesFV1 (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

Public Member Functions inherited from ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >
	IncompressibleNavierStokesBase (const char functions, const char subsets)

	IncompressibleNavierStokesBase (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

void	set_density (number val)
	sets the kinematic viscosity

void	set_stokes (bool Stokes)
	switches the convective terms off (to solve the Stokes equation)

bool	stokes ()
	flag if using Peclet Blending

void	set_laplace (bool bLaplace)
	sets assembling of diffusive term to laplace

bool	laplace ()
	flag if using Peclet Blending

void	set_peclet_blend (bool pecletBlend)
	sets if peclet blending is used in momentum equation

void	set_grad_div (number factor)
	flag if using Peclet Blending

virtual bool	requests_local_time_series ()
	returns if local time series is needed

SmartPtr< CplUserData< MathVector< dim >, dim > >	velocity ()
	returns the export of the velocity

SmartPtr< CplUserData< MathMatrix< dim, dim >, dim > >	velocity_grad ()
	returns the export of the velocity gradient

Public Member Functions inherited from ug::NavierStokes::NavierStokesBase< TDomain >
void	set_exact_jacobian (bool bExactJacobian)
	sets if the exact jacobian is computed (fixpoint approximation else)

void	set_exact_jacobian (number fullNewtonFactor)

	NavierStokesBase (const char functions, const char subsets)

	NavierStokesBase (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

void	set_kinematic_viscosity (number val)
	sets the kinematic viscosity

void	set_source (const std::vector< number > &vSource)
	sets the source function

Public Member Functions inherited from ug::IElemDisc< TDomain >
void	add_elem_modifier (SmartPtr< IElemDiscModifier< TDomain > > elemModifier)

std::vector< SmartPtr< IElemDiscModifier< TDomain > > > &	get_elem_modifier ()

	IElemDisc (const char functions, const char subsets)

	IElemDisc (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

Public Member Functions inherited from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >
virtual void	add_def_A_expl_elem (LocalVector &d, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

TLeaf &	asLeaf ()

void	check_roid (ReferenceObjectID roid, int discType)

void	do_add_def_A_elem (LocalVector &d, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_add_def_A_expl_elem (LocalVector &d, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_add_def_M_elem (LocalVector &d, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_add_jac_A_elem (LocalMatrix &J, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_add_jac_M_elem (LocalMatrix &J, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_add_rhs_elem (LocalVector &rhs, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_fsh_elem_loop ()

void	do_fsh_timestep (const number time, VectorProxyBase *u, size_t algebra_id)

void	do_fsh_timestep_elem (const number time, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_prep_elem (LocalVector &u, GridObject *elem, const ReferenceObjectID roid, const MathVector< dim > vCornerCoords[])

void	do_prep_elem_loop (const ReferenceObjectID roid, const int si)

void	do_prep_timestep (number future_time, const number time, VectorProxyBase *u, size_t algebra_id)

void	do_prep_timestep_elem (const number time, LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

virtual void	fsh_timestep (number time, VectorProxyBase *u)

virtual void	fsh_timestep_elem (const number time, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

	IElemAssembleFuncs ()

virtual void	post_assemble_loop ()

virtual void	prep_assemble_loop ()

virtual void	prep_timestep (number future_time, number time, VectorProxyBase *u)

virtual void	prep_timestep_elem (const number time, const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	set_roid (ReferenceObjectID id, int discType)

virtual	~IElemAssembleFuncs ()

Public Member Functions inherited from ug::IElemError< typename TDomain >
	IElemError (const char functions, const char subsets)

	IElemError (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

Public Member Functions inherited from ug::IElemDiscBase< typename TDomain >
SmartPtr< ApproximationSpace< TDomain > >	approx_space ()

ConstSmartPtr< ApproximationSpace< TDomain > >	approx_space () const

void	check_setup (bool bNonRegularGrid)

void	clear_imports ()

SmartPtr< TDomain >	domain ()

ConstSmartPtr< TDomain >	domain () const

const FunctionGroup &	function_group () const

ConstSmartPtr< FunctionPattern >	function_pattern () const

IDataImport< dim > &	get_import (size_t i)

	IElemDiscBase (const char functions="", const char subsets="")

	IElemDiscBase (const std::vector< std::string > &vFct, const std::vector< std::string > &vSubset)

bool	is_time_dependent () const

bool	local_time_series_needed ()

const LocalVectorTimeSeries *	local_time_solutions () const

const FunctionIndexMapping &	map () const

number	mass_scale () const

number	mass_scale () const

number	mass_scale (const size_t timePoint) const

number	mass_scale (const size_t timePoint) const

const std::vector< number > &	mass_scales () const

const std::vector< number > &	mass_scales () const

size_t	num_fct () const

size_t	num_imports () const

size_t	num_subsets () const

void	register_import (IDataImport< dim > &Imp)

void	set_approximation_space (SmartPtr< ApproximationSpace< TDomain > > approxSpace)

void	set_functions (const std::string &functions)

void	set_functions (const std::vector< std::string > &functions)

void	set_stationary ()

void	set_stationary (bool bStationaryForced=true)

void	set_subsets (const std::string &subsets)

void	set_subsets (const std::vector< std::string > &subsets)

void	set_time_dependent (LocalVectorTimeSeries &locTimeSeries, const std::vector< number > &vScaleMass, const std::vector< number > &vScaleStiff)

void	set_time_independent ()

void	set_time_point (const size_t timePoint)

number	stiff_scale () const

number	stiff_scale () const

number	stiff_scale (const size_t timePoint) const

number	stiff_scale (const size_t timePoint) const

const std::vector< number > &	stiff_scales () const

const std::vector< number > &	stiff_scales () const

TDomain::subset_handler_type &	subset_handler ()

const TDomain::subset_handler_type &	subset_handler () const

const std::vector< std::string > &	symb_fcts () const

const std::vector< std::string > &	symb_subsets () const

number	time () const

size_t	time_point () const

virtual int	type () const

virtual bool	use_hanging () const

virtual	~IElemDiscBase ()

Public Member Functions inherited from ug::IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >
TLeaf &	asLeaf ()

void	check_roid (ReferenceObjectID roid, int discType)

virtual void	compute_err_est_A_elem (const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

virtual void	compute_err_est_M_elem (const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

virtual void	compute_err_est_rhs_elem (GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

void	do_compute_err_est_A_elem (LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

void	do_compute_err_est_M_elem (LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

void	do_compute_err_est_rhs_elem (GridObject *elem, const MathVector< dim > vCornerCoords[], const number &scale)

void	do_fsh_err_est_elem_loop ()

void	do_prep_err_est_elem (LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

void	do_prep_err_est_elem_loop (const ReferenceObjectID roid, const int si)

virtual SmartPtr< IErrEstData< TDomain > >	err_est_data ()

bool	err_est_enabled () const

virtual void	fsh_err_est_elem_loop ()

	IElemEstimatorFuncs ()

virtual void	prep_err_est_elem (const LocalVector &u, GridObject *elem, const MathVector< dim > vCornerCoords[])

virtual void	prep_err_est_elem_loop (const ReferenceObjectID roid, const int si)

void	set_error_estimator (SmartPtr< IErrEstData< TDomain > > ee)

void	set_roid (ReferenceObjectID id, int discType)

virtual	~IElemEstimatorFuncs ()

Static Public Attributes
static const int	dim = base_type::dim
	World dimension.

Static Public Attributes inherited from ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >
static const int	dim = base_type::dim
	World dimension.

Static Public Attributes inherited from ug::NavierStokes::NavierStokesBase< TDomain >
static const int	dim = base_type::dim
	World dimension.

Static Public Attributes inherited from ug::IElemDisc< TDomain >
static const int	dim

Static Public Attributes inherited from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >
static const int	dim

Static Public Attributes inherited from ug::IElemError< typename TDomain >
static const int	dim

Static Public Attributes inherited from ug::IElemDiscBase< typename TDomain >
static const int	dim

Static Public Attributes inherited from ug::IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >
static const int	dim

Protected Types
typedef IncompressibleNavierStokesBase< TDomain >	base_type
	Base class type.

typedef NavierStokesFV1< TDomain >	this_type
	own type

Protected Types inherited from ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >
typedef NavierStokesBase< TDomain >	base_type
	Base class type.

typedef IncompressibleNavierStokesBase< TDomain >	this_type
	own type

Protected Types inherited from ug::NavierStokes::NavierStokesBase< TDomain >
typedef IElemDisc< TDomain >	base_type
	Base class type.

typedef NavierStokesBase< TDomain >	this_type
	own type

Protected Member Functions
virtual void	init ()


virtual void	register_all_funcs (bool bHang)

template<typename TElem , typename TFVGeom >
void	register_func ()

Protected Member Functions inherited from ug::IElemDisc< TDomain >
void	clear_add_fct ()

void	clear_add_fct (ReferenceObjectID id)

void	set_default_add_fct ()

Protected Member Functions inherited from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >
void	clear_add_fct ()

void	clear_add_fct (ReferenceObjectID id)

void	remove_add_def_A_elem_fct (ReferenceObjectID id)

void	remove_add_def_A_expl_elem_fct (ReferenceObjectID id)

void	remove_add_def_M_elem_fct (ReferenceObjectID id)

void	remove_add_jac_A_elem_fct (ReferenceObjectID id)

void	remove_add_jac_M_elem_fct (ReferenceObjectID id)

void	remove_add_rhs_elem_fct (ReferenceObjectID id)

void	remove_fsh_elem_loop_fct (ReferenceObjectID id)

void	remove_fsh_timestep_elem_fct (ReferenceObjectID id)

void	remove_fsh_timestep_fct (size_t algebra_id)

void	remove_prep_elem_fct (ReferenceObjectID id)

void	remove_prep_elem_loop_fct (ReferenceObjectID id)

void	remove_prep_timestep_elem_fct (ReferenceObjectID id)

void	remove_prep_timestep_fct (size_t algebra_id)

void	set_add_def_A_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_add_def_A_expl_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_add_def_M_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_add_jac_A_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_add_jac_M_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_add_rhs_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_default_add_fct ()

void	set_fsh_elem_loop_fct (ReferenceObjectID id, TAssFunc func)

void	set_fsh_timestep_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_fsh_timestep_fct (size_t algebra_id, TAssFunc func)

void	set_prep_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_prep_elem_loop_fct (ReferenceObjectID id, TAssFunc func)

void	set_prep_timestep_elem_fct (ReferenceObjectID id, TAssFunc func)

void	set_prep_timestep_fct (size_t algebra_id, TAssFunc func)

Protected Member Functions inherited from ug::IElemError< typename TDomain >
void	clear_add_fct ()

void	clear_add_fct (ReferenceObjectID id)

Protected Member Functions inherited from ug::IElemDiscBase< typename TDomain >
virtual void	approximation_space_changed ()

void	set_function_pattern (ConstSmartPtr< FunctionPattern > fctPatt)

void	update_function_index_mapping ()

Protected Member Functions inherited from ug::IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >
void	clear_add_fct ()

void	clear_add_fct (ReferenceObjectID id)

void	remove_compute_err_est_A_elem (ReferenceObjectID id)

void	remove_compute_err_est_M_elem (ReferenceObjectID id)

void	remove_compute_err_est_rhs_elem (ReferenceObjectID id)

void	remove_fsh_err_est_elem_loop (ReferenceObjectID id)

void	remove_prep_err_est_elem (ReferenceObjectID id)

void	remove_prep_err_est_elem_loop (ReferenceObjectID id)

void	set_compute_err_est_A_elem (ReferenceObjectID id, TAssFunc func)

void	set_compute_err_est_M_elem (ReferenceObjectID id, TAssFunc func)

void	set_compute_err_est_rhs_elem (ReferenceObjectID id, TAssFunc func)

void	set_default_add_fct ()

void	set_fsh_err_est_elem_loop (ReferenceObjectID id, TAssFunc func)

void	set_prep_err_est_elem (ReferenceObjectID id, TAssFunc func)

void	set_prep_err_est_elem_loop (ReferenceObjectID id, TAssFunc func)

Protected Attributes
bool	m_bLaplace
	flag if using only laplace term

bool	m_bPecletBlend
	flag if using Peclet Blending

bool	m_bStokes
	flag if solving the Stokes equation

SmartPtr< DataExport< MathVector< dim >, dim > >	m_exVelocity
	Export for the velocity.

SmartPtr< DataExport< MathMatrix< dim, dim >, dim > >	m_exVelocityGrad
	Export for the velocity gradient.

DataImport< number, dim >	m_imDensitySCV

DataImport< number, dim >	m_imDensitySCVF
	Data import for density.

DataImport< number, dim >	m_imKinViscosity
	Data import for kinematic viscosity.

DataImport< MathVector< dim >, dim >	m_imSourceSCV
	Data import for source.

DataImport< MathVector< dim >, dim >	m_imSourceSCVF

SmartPtr< INavierStokesFV1Stabilization< dim > >	m_spConvStab

SmartPtr< INavierStokesUpwind< dim > >	m_spConvUpwind
	Upwinding for velocity in convective term of momentum equation.

SmartPtr< INavierStokesFV1Stabilization< dim > >	m_spStab
	Stabilization for velocity in continuity equation.

Protected Attributes inherited from ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >
bool	m_bPecletBlend
	flag if using Peclet Blending

number	m_gradDivFactor
	factor for div grad stabilization

bool	m_bStokes
	flag if solving the Stokes equation

bool	m_bLaplace
	flag if using only laplace term

SmartPtr< DataExport< MathVector< dim >, dim > >	m_exVelocity
	Export for the velocity.

SmartPtr< DataExport< MathMatrix< dim, dim >, dim > >	m_exVelocityGrad
	Export for the velocity gradient.

number	m_bFullNewtonFactor
	factor for exact jacobian, (1 for exact jacobian, 0 for fix point)

Protected Attributes inherited from ug::NavierStokes::NavierStokesBase< TDomain >
number	m_bFullNewtonFactor
	factor for exact jacobian, (1 for exact jacobian, 0 for fix point)

Protected Attributes inherited from ug::IElemDisc< TDomain >
std::vector< SmartPtr< IElemDiscModifier< TDomain > > >	m_spElemModifier

Protected Attributes inherited from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >
ReferenceObjectID	m_roid

Protected Attributes inherited from ug::IElemDiscBase< typename TDomain >
bool	m_bStationaryForced

FunctionGroup	m_fctGrp

FunctionIndexMapping	m_fctIndexMap

LocalVectorTimeSeries *	m_pLocalVectorTimeSeries

SmartPtr< ApproximationSpace< TDomain > >	m_spApproxSpace

ConstSmartPtr< FunctionPattern >	m_spFctPattern

size_t	m_timePoint

std::vector< std::string >	m_vFct

std::vector< IDataImport< dim > * >	m_vIImport

std::vector< number >	m_vScaleMass

std::vector< number >	m_vScaleStiff

std::vector< std::string >	m_vSubset

Protected Attributes inherited from ug::IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >
ReferenceObjectID	m_roid

SmartPtr< IErrEstData< TDomain > >	m_spErrEstData

Static Protected Attributes
static const size_t	_P_ = dim
	abbreviation for pressure

Additional Inherited Members
Public Types inherited from ug::IElemDisc< TDomain >
typedef IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >	assemble_base_type

typedef IElemError< TDomain >	base_type

typedef TDomain	domain_type

typedef IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >	estimator_base_type

Public Types inherited from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >
typedef TDomain	domain_type

typedef TLeaf	leaf_type

Public Types inherited from ug::IElemError< typename TDomain >
typedef TDomain	domain_type

typedef IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >	estimator_base_type

Public Types inherited from ug::IElemDiscBase< typename TDomain >
typedef TDomain	domain_type

typedef TDomain::position_type	position_type

Public Types inherited from ug::IElemEstimatorFuncs< IElemDisc< TDomain >, TDomain >
typedef TDomain	domain_type

typedef TLeaf	leaf_type

Detailed Description

template<typename TDomain>
class ug::NavierStokes::NavierStokesFV1< TDomain >

Finite Volume Element Discretization for the incompressible Navier-Stokes Equation.

This class implements the IElemDisc interface to provide element local assemblings for the incompressible Navier-Stokes equation.

The unknowns of the equation are:

$ \vec{u} $ velocity
$ p $ pressure.

The equation takes the form

\begin{align*} \frac{\partial \rho \vec{u}}{\partial t} - \nabla \left( \rho \nu (\nabla \vec{u} + (\nabla \vec{u})^T) \right) + \nabla \cdot \left( \rho \vec{u} \vec{u}^T \right) + \nabla p &= \vec{f}\\ \nabla \cdot (\rho \vec{u}) &= 0 \end{align*}

with

$ \rho $ is the constant density
$ \nu $ is the kinematic viscosity (temporarily constant, implement)
$ \vec{f} \equiv f(\vec{x},t) $ is a Source Term (not implemented yet)

The first equation models the conservation of momentum and is therefore referred to as the Momentum equation. The second equation models the conservation of mass and is known as the Mass continuity equation or simply Continuity equation.

In component-wise notation, the equation reads

\begin{align*} \frac{\partial \rho u_{d_1}}{\partial t} - \sum_{d_2 = 1}^{\text{dim}} \frac{\partial}{\partial x_{d_2}} \left( \rho \nu \left( \frac{\partial u_{d_1}}{\partial x_{d_2}} + \frac{\partial u_{d_2}}{\partial x_{d_1}} \right)\right) + \sum_{d_2 = 1}^{\text{dim}} \frac{\partial}{\partial x_{d_2}} \left( \rho u_{d_2} u_{d_1} \right) + \frac{\partial p}{\partial x_{d_1}} &= f_{d_1} \qquad \forall \quad d_1 = 1, \dots, \text{dim}\\ \sum_{d = 1}^{\text{dim}} \frac{\partial \rho u_d}{\partial x_{d}} &= 0 \end{align*}

Since the density is assumed to be constant, it set to $\rho \equiv 1 $.

The finite volume element discretization uses a dual mesh consisting of Control Volumes $\mathcal{B}_h$, that cover the domain. For each control volume $B \in \mathcal{B}_h$ the following equation is solved

\begin{align*} \frac{\partial}{\partial t} \int_{B} \begin{pmatrix} \vec{u} \\ 0 \end{pmatrix} dV + \int_{\partial B} \begin{pmatrix} - \rho \nu \left(\nabla \vec{u} + (\nabla \vec{u})^T \right) \vec{n} + \vec{u} \vec{u}^T \vec{n} + p \vec{n} \\ \vec{u} \vec{n} \end{pmatrix} dS = \int_B \begin{pmatrix} \vec{f} \\ 0 \end{pmatrix} dV \end{align*}

where $ \vec{n}$ is the outer normal on the boundary of the control volume and $\int_B \cdot \; dV $ and $\int_{\partial B} \cdot \; dS $ are the integration over the control volume and the integration over the boundary of the control volume. By $f B_{sh} $f is denoted the control volume associated to a shape function (i.e. vertices, since we use P1 Lagrange ansatz functions), T usually denotes the Element.

In order to number the local unknowns, we use the following notation.

$ sh = 0, \dots, n_{sh} - 1$ loop the $n_{sh}$ shape functions. For this implementation these are the corners of the element
$ d = 0, \dots, \text{dim} - 1 $ are the velocity component of each corner
P := dim indicates the pressure component

The access to local unknowns of local vectors and matrices is now given by

\begin{align*} &\mathbf{d}(d_1, sh), \mathbf{d}(\text{\_P\_}, sh),\\ &\mathcal{J}(d_1, sh_1, d_2, sh_2), \mathcal{J}(d_1, sh_1, \text{\_P\_}, sh_2), \end{align*}

Template Parameters

TDomain	Domain
TAlgebra	Algebra

Member Typedef Documentation

◆ base_type

template<typename TDomain >

typedef IncompressibleNavierStokesBase<TDomain> ug::NavierStokes::NavierStokesFV1< TDomain >::base_type

protected

Base class type.

◆ this_type

template<typename TDomain >

typedef NavierStokesFV1<TDomain> ug::NavierStokes::NavierStokesFV1< TDomain >::this_type

protected

own type

Constructor & Destructor Documentation

◆ NavierStokesFV1() [1/2]

template<typename TDomain >

ug::NavierStokes::NavierStokesFV1< TDomain >::NavierStokesFV1	(	const char *	functions,
		const char *	subsets
	)

Constructor (setting default values)

References ug::NavierStokes::NavierStokesFV1< TDomain >::init().

◆ NavierStokesFV1() [2/2]

template<typename TDomain >

ug::NavierStokes::NavierStokesFV1< TDomain >::NavierStokesFV1	(	const std::vector< std::string > &	vFct,
		const std::vector< std::string > &	vSubset
	)

Constructor (setting default values)

References ug::NavierStokes::NavierStokesFV1< TDomain >::init().

Member Function Documentation

◆ add_def_A_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::add_def_A_elem	(	LocalVector &	d,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

adds the stiffness part to the local defect

This function adds the contribution of one element of the stiffness part to the local defect.

The local solution $ \mathbf{u} $ passes the p1 conform lagrange dofs of the element, i.e. the unknowns in the corners of the element.

Define the functional matrix of the velocity at some integration point by

\begin{align*} \nabla \vec{u}|_{ip} := \left(\left.\frac{\partial u_i}{\partial x_j} \right|_{ip}\right)_{i,j = 1,\dots,dim} \end{align*}

and the diffusive flux to

\begin{align*} \vec{f}^{\text{diff}}|_{ip} := - \nu \left( \nabla \vec{u}|_{ip} + (\nabla \vec{u}|_{ip})^T) \right) \cdot \vec{n}_{ip} \end{align*}

Suppose that a procedure producing some upwind velocity $ \vec{u}^{up}$ is available for each ip. Then, we define the convective flux to

\begin{align*} \vec{f}^{\text{conv}}|_{ip} := \left( \vec{u}^{up}|_{ip} \vec{u}^{up}|_{ip}^T \right) \cdot \vec{n}_{ip} \end{align*}

Define the pressure at the ip to be interpolated as

\begin{align*} p|_{ip} := \sum_{sh=0}^{n_{sh}-1} \mathbf{u}(\text{\_P\_}, sh) \phi_{sh} \end{align*}

The contribution added for the momentum equation is:

\begin{align*} \forall d=0,\dots, \text{dim}-1, \quad \forall sh=0,\dots, n_{sh}-1: \qquad \mathbf{d}(d, sh) &\text{ +=} \int_{\partial B_{sh} \cap T} \vec{f}^{\text{diff}}_d + \vec{f}^{\text{conv}}_d + p \vec{n}_d \;dS \approx \sum_{i=1}^{n_{\partial B_{sh}}} |\partial B^i_{sh} \cap T| \left( \left.\vec{f}^{\text{diff}}_d\right|_{ip} + \left.\vec{f}^{\text{conv}}_d\right|_{ip} + p|_{ip} \vec{n}|_{ip} \right)\\ \end{align*}

Assume, that some stabilized velocity $ \vec{u}^{stab}$ is available for each ip. Then, the contribution added for the continuity equation is:

\begin{align*} \forall sh=0,\dots, n_{sh}-1: \qquad \mathbf{d}(\text{\_P\_}, sh) &\text{ +=} \int_{\partial B_{sh} \cap T} \vec{u}^{stab} \cdot \vec{n} \;dS \approx \sum_{i=1}^{n_{\partial B_{sh}}} |\partial B^i_{sh} \cap T| \; \vec{u}^{stab}|_{ip} \cdot \vec{n}|_{ip}\\ \end{align*}

Parameters

[in,out]	d	local defect with values added on output
[in]	u	local vector of current solution
[in]	time	current time step

Template Parameters

TElem	Element type
TFVGeom	Finite Volume Geometry

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), ug::MatVecMult(), ug::LocalVectorTimeSeries::size(), ug::LocalVectorTimeSeries::solution(), ug::NavierStokes::INavierStokesFV1Stabilization< dim >::stab_vel(), ug::LocalVectorTimeSeries::time(), ug::TransposedMatVecMultAdd(), UG_ASSERT, UG_THROW, ug::NavierStokes::INavierStokesUpwind< dim >::upwind_vel(), ug::VecProd(), ug::VecScale(), and ug::VecSet().

◆ add_def_M_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::add_def_M_elem	(	LocalVector &	d,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

adds the mass part to the local defect

This function adds the contribution of one element of the mass part to the local defect.

The local solution $ \mathbf{u} $ passes the p1 conform lagrange dofs of the element, i.e. the unknowns in the corners of the element.

The contribution added is:

\begin{align*} \forall d=0,\dots, \text{dim}-1, \quad \forall sh=0,\dots, n_{sh}-1: \qquad \mathbf{d}(d, sh) &\text{ +=} \int_{B_{sh} \cap T} \vec{u}_d dV \approx |B_{sh} \cap T| \mathbf{u}(d, sh)\\ \mathbf{d}(\text{\_P\_, sh}) &\text{ +=} 0 \end{align*}

Parameters

[in,out]	d	local defect with values added on output
[in]	u	local vector of current solution
[in]	time	current time step

Template Parameters

TElem	Element type
TFVGeom	Finite Volume Geometry

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), and UG_ASSERT.

◆ add_jac_A_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::add_jac_A_elem	(	LocalMatrix &	J,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

adds the stiffness part to the local jacobian

This function adds the local contributions of the stiffness part to the local jacobian.

For the definition of $ \vec{f}^{\text{diff}}|_{ip}$ and $ \vec{f}^{\text{conv}}|_{ip}$ see add_def_A_elem.

The derivative of the diffusive flux is given by

\begin{align*} \frac{\partial \vec{f}^{\text{diff}}_{d_1}|_{ip}}{\partial \vec{u}_{d_2}^{sh}} &= - \nu \left( \delta_{d_1, d_2} \sum_{k=1}^{\text{dim}} \left. \frac{\partial \phi^{sh}}{\partial x_k}\right|_{ip} \vec{n_k}|_{ip} + \left. \frac{\partial \phi^{sh}}{\partial x_{d_1}}\right|_{ip} \vec{n_{d_2}}|_{ip} \right)\\ \frac{\partial \vec{f}^{\text{diff}}_{d_1}|_{ip}}{\partial p^{sh}} &= 0 \end{align*}

For the derivative of the convective term, we can use a fixpoint linearization if we only differentiate the first factor of $ \vec{f}^{\text{conv}}_{d_1} = (\vec{u}^{\text{blend}} (\vec{u}^{\text{blend}})^T)_{d_1 k} \vec{n}_k = \vec{u}^{\text{blend}}_{d_1} \sum_{k=1}^{\text{dim}} \vec{u}^{\text{blend}}_k \vec{n}_k = \vec{u}^{\text{blend}}_{d_1} \langle \vec{u}^{\text{blend}}, \vec{n} \rangle $

This gives

\begin{align*} \frac{\partial \vec{f}^{\text{conv}}_{d_1}}{\partial \vec{u}_{d_2}^{sh}} &= \langle \vec{u}^{\text{blend}}, \vec{n} \rangle \frac{\partial \vec{u}^{\text{blend}}_{d_1}}{\partial \vec{u}_{d_2}^{sh}} &= \langle \vec{u}^{\text{blend}}, \vec{n} \rangle \left( (1-\omega) \delta_{d_1 d_2} \phi^{sh} + \omega \frac{\partial \vec{u}^{\text{up}}_{d_1}}{\partial \vec{u}_{d_2}^{sh}} \right) \end{align*}

The derivative of the pressure term is given by

\begin{align*} \frac{\partial p \vec{n}|_{ip}}{\partial \vec{u}_{d_2}^{sh}} &= 0\\ \frac{\partial p \vec{n}|_{ip}}{\partial p^{sh}} &= \phi^{sh}|_{ip} \vec{n} \end{align*}

The derivative of the continuity term is given by

\begin{align*} \frac{\partial \vec{u}^{\text{stab}}|_{ip} \vec{n}|_{ip}}{\partial \vec{u}_{d_1}^{sh}} &= \sum_{d_2=1}^{dim} \left. \frac{\partial u_{d_2}^{\text{stab}}} {\partial \vec{u}_{d_1}^{sh}} \right|_{ip} \vec{n}_{d_2}\\ \frac{\partial \vec{u}^{\text{stab}}|_{ip} \vec{n}|_{ip}}{\partial p^{sh}} &=\sum_{d_2=1}^{dim} \left. \frac{\partial u_{d_2}^{\text{stab}}} {\partial p^{sh}} \right|_{ip} \vec{n}_{d_2}\\ \end{align*}

Parameters

[in,out]	J	local jacobian with values added on output
[in]	u	local vector of current solution
[in]	time	current time step

Template Parameters

TElem	Element type
TFVGeom	Finite Volume Geometry

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), ug::LocalVectorTimeSeries::size(), ug::LocalVectorTimeSeries::solution(), ug::NavierStokes::INavierStokesFV1Stabilization< dim >::stab_shape_p(), ug::NavierStokes::INavierStokesFV1Stabilization< dim >::stab_shape_vel(), ug::NavierStokes::INavierStokesFV1Stabilization< dim >::stab_vel(), ug::LocalVectorTimeSeries::time(), UG_ASSERT, UG_THROW, ug::NavierStokes::INavierStokesUpwind< dim >::upwind_shape_ip(), ug::NavierStokes::INavierStokesUpwind< dim >::upwind_shape_sh(), ug::NavierStokes::INavierStokesUpwind< dim >::upwind_vel(), ug::VecDot(), ug::VecProd(), ug::VecSet(), and ug::NavierStokes::INavierStokesFV1Stabilization< dim >::vel_comp_connected().

◆ add_jac_M_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::add_jac_M_elem	(	LocalMatrix &	J,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

adds the mass part to the local jacobian

This function adds the contribution of one element of the mass part to the local jacobian.

The local solution $ \mathbf{u} $ passes the p1 conform lagrange dofs of the element, i.e. the unknowns in the corners of the element.

The contribution added is:

\begin{align*} \forall d=0,\dots, \text{dim}-1, \quad \forall sh=0,\dots, n_{sh}-1: \qquad \mathcal{J}(d, sh, d, sh) &\text{ +=} \int_{B_{sh} \cap T} dV = |B_{sh} \cap T|\\ \end{align*}

Parameters

[in,out]	J	local jacobian with values added on output
[in]	u	local vector of current solution
[in]	time	current time step

Template Parameters

TElem	Element type
TFVGeom	Finite Volume Geometry

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), and UG_ASSERT.

◆ add_rhs_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::add_rhs_elem	(	LocalVector &	d,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

adds the source part to the local defect

This function adds the contribution of one element of the source part to the local defect, if a source function $ \vec{f} $ has been specified. Otherwise a zero source function is assumed.

The contribution added is:

\begin{align*} \forall d=0,\dots, \text{dim}-1, \quad \forall sh=0,\dots, n_{sh}-1: \qquad \mathbf{d}(d, sh) &\text{ +=} \int_{B_{sh} \cap T} \vec{f}_d \; dV \approx |B_{sh} \cap T| \; \vec{f}_d|_{ip} \end{align*}

Parameters

[in,out]	d	local defect with values added on output
[in]	time	current time step

Template Parameters

TElem	Element type
TFVGeom	Finite Volume Geometry

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), and UG_ASSERT.

◆ density()

template<typename TDomain >

SmartPtr< CplUserData< number, dim > > ug::NavierStokes::NavierStokesFV1< TDomain >::density ( )

inlinevirtual

returns density

Implements ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >.

References ug::NavierStokes::NavierStokesFV1< TDomain >::m_imDensitySCVF, and ug::DataImport< typename TData, int dim >::user_data().

◆ disc_type()

template<typename TDomain >

virtual std::string ug::NavierStokes::NavierStokesFV1< TDomain >::disc_type ( ) const

inlinevirtual

returns string identifying disc type

Implements ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >.

◆ ex_nodal_velocity()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::ex_nodal_velocity	(	MathVector< dim >	vValue[],
		const MathVector< dim >	vGlobIP[],
		number	time,
		int	si,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[],
		const MathVector< TFVGeom::dim >	vLocIP[],
		const size_t	nip,
		bool	bDeriv,
		std::vector< std::vector< MathVector< dim > > >	vvvDeriv[]
	)

export value of the velocity

References ug::GeomProvider< typename TGeom >::get(), ug::BaseLSFS< typename TImpl, int TDim, typename TShape, typename TGrad >::shapes(), and ug::VecSet().

◆ ex_velocity_grad()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::ex_velocity_grad	(	MathMatrix< dim, dim >	vValue[],
		const MathVector< dim >	vGlobIP[],
		number	time,
		int	si,
		const LocalVector &	u,
		GridObject *	elem,
		const MathVector< dim >	vCornerCoords[],
		const MathVector< TFVGeom::dim >	vLocIP[],
		const size_t	nip,
		bool	bDeriv,
		std::vector< std::vector< MathMatrix< dim, dim > > >	vvvDeriv[]
	)

computes the value of the gradient of the velocity

References ug::GeomProvider< typename TGeom >::get(), ug::BaseLSFS< typename TImpl, int TDim, typename TShape, typename TGrad >::grads(), and ug::MatSet().

◆ fsh_elem_loop()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::fsh_elem_loop ( )

virtual

finishes the element loop

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

◆ init()

template<typename TDomain >

void ug::NavierStokes::NavierStokesFV1< TDomain >::init ( )

protectedvirtual

References UG_THROW.

Referenced by ug::NavierStokes::NavierStokesFV1< TDomain >::NavierStokesFV1(), and ug::NavierStokes::NavierStokesFV1< TDomain >::NavierStokesFV1().

◆ kinematic_viscosity()

template<typename TDomain >

SmartPtr< CplUserData< number, dim > > ug::NavierStokes::NavierStokesFV1< TDomain >::kinematic_viscosity ( )

inlinevirtual

returns kinematic viscosity

Implements ug::NavierStokes::IncompressibleNavierStokesBase< TDomain >.

References ug::NavierStokes::NavierStokesFV1< TDomain >::m_imKinViscosity, and ug::DataImport< typename TData, int dim >::user_data().

◆ peclet_blend()

template<typename TDomain >

template<typename TFVGeom >

number ug::NavierStokes::NavierStokesFV1< TDomain >::peclet_blend	(	MathVector< dim > &	UpwindVel,
		const TFVGeom &	geo,
		size_t	ip,
		const MathVector< dim > &	StdVel,
		number	kinVisco
	)

inline

computes the pecled blended Upwind veloctity

This function compute the peclet blended velocity. First, the standard interpolated (no upwind) velocity is computed at the integration point of the scvf:

\begin{align*} \vec{u}^{\text{std}}_d|_{ip} := \sum_{sh=0}^{n_{sh}-1} \mathbf{u}(d, sh) \; \phi_{sh} \end{align*}

Defining the Peclet Number

\begin{align*} Pe := \frac{\vec{u}^{\text{std}}|_{ip} \cdot \vec{n}|_{ip} \; L}{\nu} \end{align*}

with the Viscosity $ \nu $ and the diffusion length $ L $, a weighting factor is computed:

\begin{align*} \omega := \frac{Pe^2}{5 + Pe^2} \end{align*}

and the blended velocity is computed to

\begin{align*} \vec{u}^{\text{blend}}|_{ip} := \omega \vec{u}^{\text{up}} + (1-\omega) \vec{u}^{\text{std}} \end{align*}

Parameters

[in,out]	UpwindVel	upwind vel on entry, blended vel on exit
[in]	scvf	SubControlVolumeFace of the Velocity
[in]	StdVel	standard interpolation vel
[in]	kinVisco	kinematic Viscosity at scvf

Returns: $\omega$ weighting factor

References ug::VecDistance(), ug::VecProd(), ug::VecScaleAdd(), and ug::VecTwoNormSq().

◆ prep_elem()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::prep_elem	(	const LocalVector &	u,
		GridObject *	elem,
		const ReferenceObjectID	roid,
		const MathVector< dim >	vCornerCoords[]
	)

virtual

prepares the element for evaluation

This function prepare a specific element for assembling. This function is always called before any of the assemble_... functions is performed. Here, the Finite Volume Geometry is prepared and global positions of the evaluation points of the DataImports are requested (and local positions in case of hanging node assembling)

Parameters

[in]	elem	element to prepare the data for
[in]	u	current local solution vector
[in]	glob_ind	global indices of the local vector components

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), subset_handler(), and UG_CATCH_THROW.

◆ prep_elem_loop()

template<typename TDomain >

template<typename TElem , typename TFVGeom >

void ug::NavierStokes::NavierStokesFV1< TDomain >::prep_elem_loop	(	const ReferenceObjectID	roid,
		const int	si
	)

virtual

prepares the element loop

This function is used to prepare the element loop. It gets called, before the loop over all elements starts. Here, general checks are performed:

Is the correct finite volume geometry used
Has the stabilization been specified

In addition, local coordinates of evaluation points are requested by the DataImports in case of element-fixed points.

Reimplemented from ug::IElemAssembleFuncs< IElemDisc< TDomain >, TDomain >.

References ug::GeomProvider< typename TGeom >::get(), and UG_THROW.

◆ prepare_setting()

template<typename TDomain >

void ug::NavierStokes::NavierStokesFV1< TDomain >::prepare_setting	(	const std::vector< LFEID > &	vLfeID,
		bool	bNonRegularGrid
	)

virtual

type of trial space for each function used

Implements ug::IElemDiscBase< typename TDomain >.

References ug::LFEID::LAGRANGE, type(), and UG_THROW.

void ug::NavierStokes::NavierStokesFV1< TDomain >::set_upwind ( SmartPtr< INavierStokesFV1Stabilization< dim > > spStab )

inline

sets a stabilization for upwinding (Physical Advection Correction)

References ug::NavierStokes::NavierStokesFV1< TDomain >::m_spConvStab, ug::NavierStokes::NavierStokesFV1< TDomain >::m_spConvUpwind, and SPNULL.

Referenced by ug::NavierStokes::NavierStokesFV1< TDomain >::set_pac_upwind().

◆ set_upwind() [3/3]

template<typename TDomain >

void ug::NavierStokes::NavierStokesFV1< TDomain >::set_upwind ( SmartPtr< INavierStokesUpwind< dim > > spUpwind )

inline

sets an upwinding for the convective term of momentum equation

References ug::NavierStokes::NavierStokesFV1< TDomain >::m_spConvStab, ug::NavierStokes::NavierStokesFV1< TDomain >::m_spConvUpwind, and SPNULL.

◆ sourceSCVF()

template<typename TDomain >

DataImport< MathVector< dim >, dim > ug::NavierStokes::NavierStokesFV1< TDomain >::sourceSCVF ( )

inline

returns scvf source

References ug::NavierStokes::NavierStokesFV1< TDomain >::m_imSourceSCVF.

◆ stabilization()

template<typename TDomain >

SmartPtr< INavierStokesFV1Stabilization< dim > > ug::NavierStokes::NavierStokesFV1< TDomain >::stabilization ( )

template<typename TDomain >

DataImport<number, dim> ug::NavierStokes::NavierStokesFV1< TDomain >::m_imKinViscosity

protected

Data import for kinematic viscosity.

Referenced by ug::NavierStokes::NavierStokesFV1< TDomain >::kinematic_viscosity().

◆ m_imSourceSCV

template<typename TDomain >

DataImport<MathVector<dim>, dim> ug::NavierStokes::NavierStokesFV1< TDomain >::m_imSourceSCV

protected

Data import for source.

template<typename TDomain >

SmartPtr<INavierStokesFV1Stabilization<dim> > ug::NavierStokes::NavierStokesFV1< TDomain >::m_spStab

protected

Stabilization for velocity in continuity equation.

Referenced by ug::NavierStokes::NavierStokesFV1< TDomain >::set_pac_upwind(), ug::NavierStokes::NavierStokesFV1< TDomain >::set_stabilization(), ug::NavierStokes::NavierStokesFV1< TDomain >::set_stabilization(), ug::NavierStokes::NavierStokesFV1< TDomain >::set_stabilization(), ug::NavierStokes::NavierStokesFV1< TDomain >::set_upwind(), and ug::NavierStokes::NavierStokesFV1< TDomain >::stabilization().

The documentation for this class was generated from the following files:

/home/runner/work/docs/docs/ug4/plugins/NavierStokes/incompressible/fv1/navier_stokes_fv1.h
/home/runner/work/docs/docs/ug4/plugins/NavierStokes/incompressible/fv1/navier_stokes_fv1.cpp

Public Member Functions

Static Public Attributes

Protected Types

Protected Member Functions

Protected Attributes

Static Protected Attributes

Additional Inherited Members

Detailed Description

Member Typedef Documentation

◆ base_type

◆ this_type

Constructor & Destructor Documentation

◆ NavierStokesFV1() [1/2]

◆ NavierStokesFV1() [2/2]

Member Function Documentation

◆ add_def_A_elem()

◆ add_def_M_elem()

◆ add_jac_A_elem()

◆ add_jac_M_elem()

◆ add_rhs_elem()

◆ density()

◆ disc_type()

◆ ex_nodal_velocity()

◆ ex_velocity_grad()

◆ fsh_elem_loop()

◆ init()

◆ kinematic_viscosity()

◆ peclet_blend()

◆ prep_elem()

◆ prep_elem_loop()

◆ prepare_setting()

◆ register_all_funcs()

◆ register_func()

◆ set_density()

◆ set_kinematic_viscosity()

◆ set_pac_upwind()

◆ set_source()

◆ set_stabilization() [1/3]

◆ set_stabilization() [2/3]

◆ set_stabilization() [3/3]

◆ set_upwind() [1/3]

◆ set_upwind() [2/3]

◆ set_upwind() [3/3]

◆ sourceSCVF()

◆ stabilization()

Member Data Documentation

◆ _P_

◆ dim

◆ m_bLaplace

◆ m_bPecletBlend

◆ m_bStokes

◆ m_exVelocity

◆ m_exVelocityGrad

◆ m_imDensitySCV

◆ m_imDensitySCVF

◆ m_imKinViscosity

◆ m_imSourceSCV

◆ m_imSourceSCVF

◆ m_spConvStab

◆ m_spConvUpwind

◆ m_spStab