For Discretizations, the discrete functions (sometimes also called "grid functions", since they "live" on the grid) have to be specified. This is done by the use of a Function Pattern.

Function Pattern

A Function Pattern has an underlying ISubsetHandler. The Subset Handler defines the subset of the grids, where functions can be defined independently. Thus, given a Grid, it is intended, that the user chooses appropriate subsets of the grid for his problem. Then, he can assign discrete functions on this subset partition.

It is possible to define functions:

on all subsets, i.e. on the whole grid
just on one subset
on a union of subsets.

Each discrete function (regardless if defined on unions of subsets or the whole grid) gets a unique function id. The Function Pattern knows how many functions are defined in total (i.e. on all subsets) and also knows how many functions are defined on one subset.

Function Group

Often a subset of functions is needed from a Function Pattern. This arise, e.g., for

all functions of a subset
all functions for a element discretization
...

In order to facilitate the usage, one can use the Function Group. This class needs the underlying Function Pattern to choose the functions from. Then, functions can be chosen to be part of the Function Group by simply selecting the name or the unique id. Having chosen a subset of functions, the Function Group can tell the user a lot of information:

\( N^f \):= the number of selected functions
the unique id of the i'th chosen function ( \( i \in [0, ..., N^f -1] \))
if a function with global id is contained in the function group
...

Important: The order in which the Functions are selected is crucial. In this order the selected function appear in the Function Group. The functions are NOT sorted by unique id, or something like that. This is important, since a Function Group will be used to describe the functions used for the IElemDisc and there the order is crucial. E.g. for d3f, we need to specify "Concentration" and "Pressure", in this order. Thus, passing the function, representing the concentration first is crucial. However, if explicitly wanted by the user, the functions can be sorted by invoking the sort-method of the function group.

Unions of Function Groups

It is easily possible to construct Unions of FunctionsGroups, which is a Function Group by itself. Starting with an empty FunctionGroup one can simply add all the Function Groups of the union. All not already registered functions are then added to the Union. Note, that the order is defined by the order of adding the Function Groups. From a computational view their is no difference between a FunctionGroup and a Union, its the usage of the user, that makes the difference.

Function Index Mapping

Given a Union of Function Groups and one Function Group, that is contained in the Union, a common task is to find the mapping between the local ids of the Function Group and the local ids of the same function in the Union.

To facilitate this task the FunctionIndexMapping can be used. It is simply a vector holding the local id of the function in the Union for each local id in the FunctionGroup.

This can be used to create a mapping with fctGroup[i] == unionGroup[ map[i] ] for all entries of the function group.

Function Group Example

Here is an example:

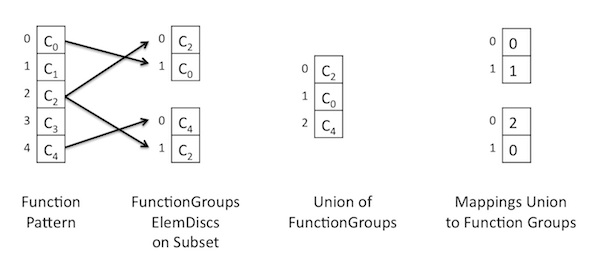
Imagine, we have 5 functions. Let's name these functions for simplicity by \( c_0, \ldots, c_4 \). Now, in the function pattern, each function has a unique id (in our case \(i\) for the function with name \( c_i \)).

If we define 2 Element Discretizations, that work on 2 funtions each, these two Disc will create their own Function Group of the functions they work on. Keep in mind, that here the order of the functions is crutial. For example, the first Discretization works on function \(c_2\) as its local function of index 0 and has function \(c_0\) as a local function of index 1.

Now, one can have the union of the functions of both ElemDiscs. This will lead to a Function group of the three common functions of the elem discs.

Finally, one may want a mapping between the local index of the ElemDisc Function Groups and the Union Function Group. This is shown on the right. Lets focus on the second element disc. Here the function with local index 0 is the function with unique id 4. This function has in the union Function Group the local index 2. Thus, the mapping has the entry (local index 0 -> local index 2).